
[← pTRM check statistics] [↑ SPD on the web] [Additivity check statistics →]
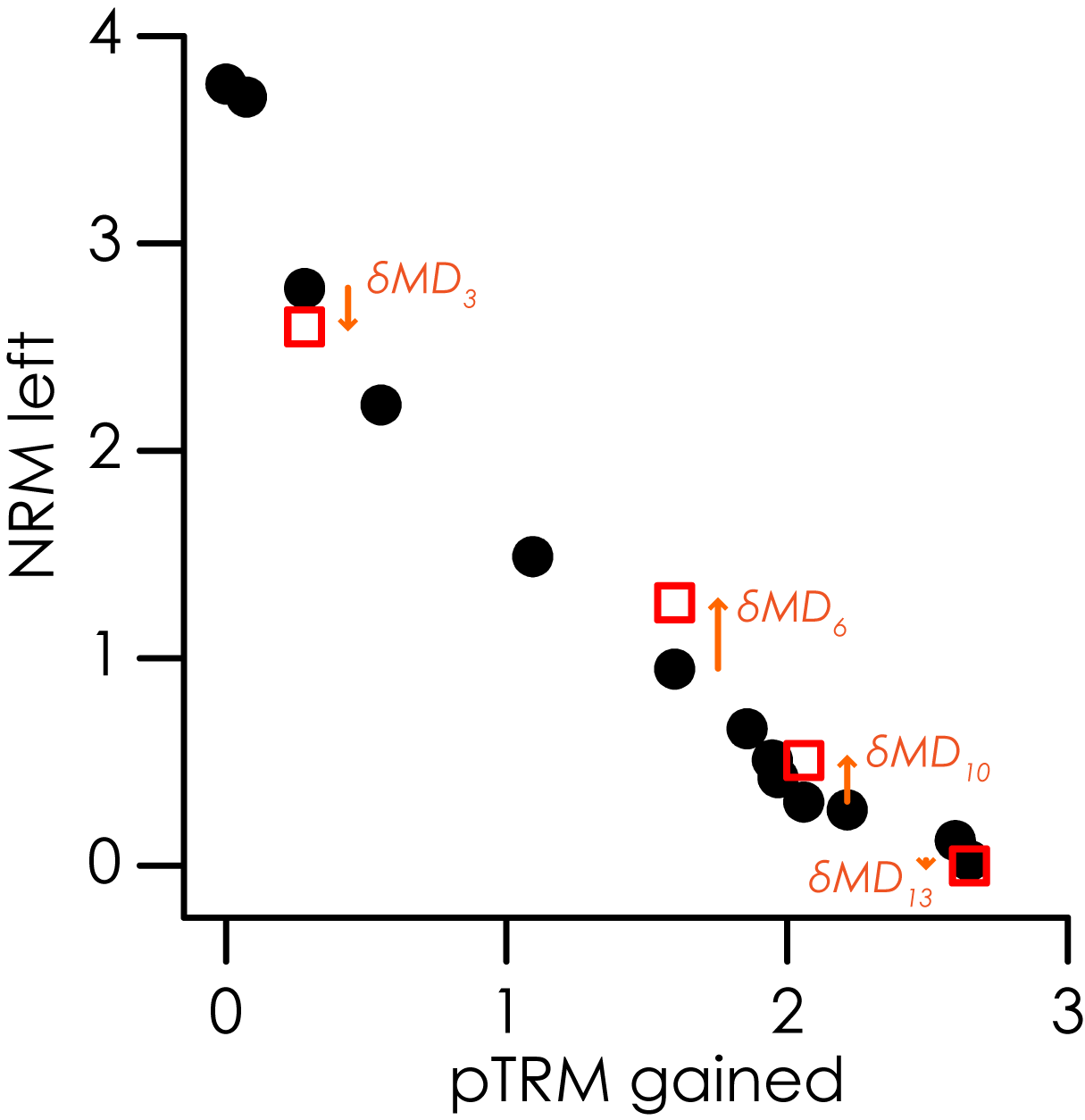
A pTRM tail check is a repeat demagnetization step to test for changes in a specimen's magnetization carried in the blocking temperature range above the temperature of the check. The difference between the first NRM measurement and the pTRM tail check is calculated as the scalar intensity difference: \[ \delta{tail_i}=tail\_check_i - NRM_i = tail\_check_i - y_i, \] where $$tail\_check_i$$ is the pTRM tail check to the $$i^{th}$$ temperature step. The order of the difference is such that tail checks smaller than the original NRM yield negative $\delta{tail_i}$ and tail checks larger than the original NRM give positive $\delta{tail_i}$. For a pTRM tail check to be included in the analysis, $$T_i$$ must be less than or equal to $$T_{max}$$.
Statistic: $$n_{Tail}$$
The number of pTRM tail checks conducted below the maximum temperature used for the best-fit segment on the Arai plot (i.e., the number of pTRM tail checks used to analyze the best-fit segment on the Arai plot).
Statistic: $$DRAT_{Tail}$$
Report to 1 d.p.
Maximum absolute difference produced by a pTRM tail check, normalized by the length of the best-fit line (Biggin et al., 2007). \[ DRAT_{Tail}=\frac{\max{\{\left| \delta{tail_i} \right|\}}_{i=1, \ldots, end}}{L}\times{100} \]
Statistic: $$\delta{TR}$$
Report to 1 d.p.
Maximum absolute difference produced by a pTRM tail check, normalized by the NRM (obtained from the intersection of the best-fit line and the y-axis on an Arai plot; Leonhardt et al., 2004a). \[ \delta{TR}=\frac{\max{\{\left| \delta{tail_i} \right|\}}_{i=1, \ldots, end}}{\left|Y_{Int.}\right|}\times{100} \]
Statistic: $$MD_{VDS}$$
Report to 1 d.p.
Maximum absolute difference produced by a pTRM tail check, normalized by the vector difference sum of the NRM (Tauxe and Staudigel, 2004). \[ MD_{VDS}=\frac{\max{\{\left| \delta{tail_i} \right|\}}_{i=1, \ldots, end}}{VDS}\times{100} \]
Useful Note...
Some versions of PmagPy and ThellierGUI use a pTRM tail check statistic called $$MD(\%)$$.
This is identical to $$MD_{VDS}$$, but the change in name emphasizes its calculation method.
Statistic: $$\delta{t^*}$$
Report to 1 d.p.
The extent of a pTRM tail after correction for angular dependence (Leonhardt et al., 2004a; 2004b).
The applied laboratory field vector ($$\mathbf{B}_{Lab}$$) is typically applied along a principle axis in the sample coordinate system (i.e., $$\pm x$$, $$\pm y$$, or $$\pm z$$). Therefore, for simplicity, $$\delta{t^*}$$ should be calculated in the sample coordinate system only. Figure 7 is a schematic illustration of aspects of the calculation of $$\delta{t^*}$$.

Let $$N_{x,i}$$, $$N_{y,i}$$, and $$N_{z,i}$$ denote the Cartesian coordinates of the NRM vector at step $$i$$ (i.e., $$\mathbf{NRM}_i = $$ [$$N_{x,i}$$, $$N_{y,i}$$, $$N_{z,i}$$]). Similarly, let $$T_{x,i}$$, $$T_{y,i}$$, and $$T_{z,i}$$ denote the Cartesian coordinates of the repeat demagnetization vector at step $$i$$ (i.e., $$\mathbf{tail\_check}_i = $$ [$$T_{x,i}$$, $$T_{y,i}$$, $$T_{z,i}$$]).
Assuming that $$\mathbf{B}_{Lab}$$ is applied along the z-axis, the difference in the horizontal ($$\delta{H_i}$$) and vertical components ($$\delta{Z_i}$$) between $$\mathbf{NRM}_i$$ and $$\mathbf{tail\_check}_i$$ (Figure 7) are given by: \[ \delta{H_i}=\sqrt{N_{x,i}^2 + N_{y,i}^2} - \sqrt{T_{x,i}^2 + T_{y,i}^2} \] and \[ \delta{Z_i}=N_{z,i} - T_{z,i}. \]
pTRM tails have an angular dependence and the calculation of $$\delta{t^*}$$ requires two angular differences. Let $$\Delta{\theta}_i$$ denote the angle between $$\mathbf{B}_{Lab}$$ and $$\mathbf{NRM}_i$$ (see Section 4 for advice on calculating the angle between two vectors). Let $$\delta{Inc}_i$$ denote the difference in inclinations between the $$\mathbf{B}_{Lab}$$ and $$\mathbf{NRM}_i$$: \[ \delta{Inc_i}=Inc(\mathbf{B}_{Lab}) - Inc(\mathbf{NRM}_i)=\arctan{\left(\frac{B_{Lab,z}}{\sqrt{B_{Lab,x}^2 + B_{Lab,y}^2}}\right)} - \arctan{\left(\frac{N_{z,i}}{\sqrt{N_{x,i}^2 + N_{x,i}^2}}\right)}. \] In the ThellierTool software (v4.22 and previous) $$\mathbf{B}_{Lab}$$ is determined from each $$\mathbf{TRM}_i$$. Given that $$\mathbf{B}_{Lab}$$ is almost always known, the convention of SPD is to use the known $$\mathbf{B}_{Lab}$$ and not as estimated from $$\mathbf{TRM}_i$$, which may suffer from the effects of experimental noise.
As will be seen below, the calculation of $$\delta{t^*}$$ requires $$\frac{1}{\tan{(\Delta{\theta}_i)}}$$. As $$\Delta{\theta}_i$$ approaches zero or 180° this fraction tends to infinity. To tackle this, $$\delta{t^*}$$ is calculated in a piecewise fashion that depends on upper and lower angular limits ($$Lim_{upper}$$ and $$Lim_{lower}$$, respectively). Below is pseudo-code that describes the logic of the calculation procedure.
if $$\Delta{\theta}_i < Lim_{upper}$$ and $$\Delta{\theta}_i > Lim_{lower}$$ then
if $$\delta{Inc_i} > 0$$ then
$$t^*_i=100\times\left|b\right| \frac{ -\delta{Z_i} + \frac{\delta{H_i}}{\tan{(\Delta{\theta}_i)}} }{\left|Y_{Int.}\right|}$$
else
$$t^*_i=100\times\left|b\right| \frac{ \delta{Z_i} - \frac{\delta{H_i}}{\tan{(\Delta{\theta}_i)}} }{\left|Y_{Int.}\right|}$$
end if
else
if $$\Delta{\theta}_i \leq Lim_{lower}$$ then
$$t^*_i=0$$
else if $$\Delta{\theta}_i \geq Lim_{upper}$$ then
$$t^*_i=100\times\frac{-\delta{Z_i}}{\left|X_{Int.}\right|+\left|Y_{Int.}\right|}$$
end if
end if
In v4.22 of the ThellierTool $$Lim_{lower} = 0.175$$ ($$\approx10$$°) radians and $$Lim_{upper} = 2.968$$ radians($$\approx170$$°). These are adopted here.
$$\delta{t^*}$$ is then calculated as: \[ \delta{t^*}=\left\{ \begin{array}{lc} \max{ \left\{ t^*_i\right\} }_{i=1, \ldots, end} & \mbox{ if } (\max{ \left\{ t^*_i\right\} }_{i=1, \ldots, end} > 0)\\ 0 & \mbox{ if } (\max{ \left\{ t^*_i\right\} }_{i=1, \ldots, end} < 0)\end{array}\right. \] Only positive values of $$t^*$$ and $$\delta{t^*}$$ can be attributed to the effects of pTRM tails, hence $$\delta{t^*}$$ is calculated as the maximum of $$t^*$$ and not the maximum of $$\left|t^*\right|$$.
It should be noted that an implicit assumption in the above calculations is that $$\mathbf{B}_{Lab}$$ is applied along the $$z$$-axis. In situations where $$\mathbf{B}_{Lab}$$ is applied along the $$x$$- or $$y$$-axes, the definition of ``horizontal'' and ``vertical'' can be redefined such that $$\mathbf{B}_{Lab}$$ is applied in the ``vertical'' direction. For example, if $$\mathbf{B}_{Lab}$$ is along the $$x$$-axis, $$\delta{H_i}$$ and $$\delta{Z_i}$$ can be defined as: \[ \delta{H_i}=\sqrt{N_{y,i}^2 + N_{z,i}^2} - \sqrt{T_{y,i}^2 + T_{z,i}^2} \] and \[ \delta{Z_i}=N_{x,i} - T_{x,i}, \] and \[ \delta{Inc_i}=\arctan{\left(\frac{B_{Lab,x}}{\sqrt{B_{Lab,y}^2 + B_{Lab,z}^2}}\right)} - \arctan{\left(\frac{N_{x,i}}{\sqrt{N_{y,i}^2 + N_{z,i}^2}}\right)}. \] The remaining calculations can proceed as described above.
↑ TOP